PAT Breakdown #3: All about angle ranking
This pre-dental blog is brought to you by Crack the DAT. Crack the DAT offers all the resources you need to ace your Dental Admission Test, all in one place! Try it today: CrackDAT.com
On the Perceptual Ability Test (PAT section) of the Dental Admission Test, you’ll encounter six question types that assess your spatial and visual reasoning skills. One of these question types is angle ranking. Read on to learn all about angle ranking and to learn strategies that will help you breeze through these questions with confidence!
What to expect
On the the Dental Admission Test (DAT), you will have a total of 15 angle ranking questions (#31–45 of the PAT section). You will see four angles, which may be obtuse, acute, or right angles. These angles may appear similar at first glance, but the measure of their interior angles will vary by a few degrees. Your goal is to rank the interior angles, from smallest to largest. Here’s an example of an angle ranking question you might see on the DAT:

In this case, the correct ranking of the angles is 4-2-1-3, meaning that Angle 4 is the smallest and Angle 3 is the largest. You’ll have four multiple choice answers to choose from on the angle ranking section.
The rules
The rules for this section are simple:
- You’ll always be choosing the answer choice that correctly orders the angles from smallest to largest.
- The angles can be rotated any which way, and their side lengths may vary. The angles might be scaled differently, too. Don’t let this confuse you — you only need to focus on the measure of the interior angles.
The strategies
- Practice makes perfect. It’s true for every PAT question type! With time and practice, you will be able to discern increasingly small differences in the interior angle measurements. Do practice sets, use the angle ranking generator on CrackDAT.com, and download the CrackDAT app to practice in your spare time. You will improve your speed and accuracy as you familiarize yourself with angle ranking, so set aside at least 10–15 minutes each day to practice and learn from your mistakes, and don’t give up!
- Use a visualization technique. The goal of these techniques is to visualize the angles in a way that allows you to more easily discern their differences. Here are some techniques — see if any of them work for you. Also note that you don’t need to use the same technique each time. No technique is foolproof or guaranteed to help with every question, but with an arsenal of 2–4 techniques that work for you, you’re more likely to be able to figure out the correct answer.
Laptop method

Imagine that all of the angles are laptops viewed from the side. One half of the angle represents the laptop’s keyboard/base, while the other half represents the screen/top half. Now, try to determine which “laptop” is most closed, and which is widest open. The more open the “laptop,” the larger the angle. The more closed, the smaller the angle. This is a great method for visualizing the angles in a new way and connecting them to familiar, real-life objects.
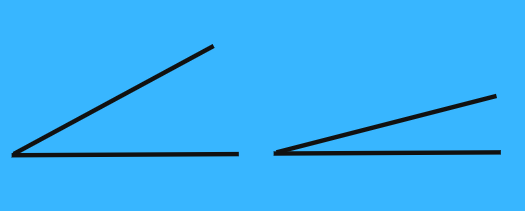
Paper cup method

Imagine that the angles are cone-shaped paper cups (like the water cups often found at dental offices). Which “cup” would hold the largest volume of water? The larger or wider the “cup” — that is, the larger the interior angle — the more water inside. The smaller or narrower the “cup,” the less water held inside. Like the laptop method, this method can be beneficial because it requires you to visualize the angles as familiar, real-life objects.
Angle fitting method

This method requires you to visualize which angles would be able to fit inside each other. Look at the two angles above. Which angle could fit inside the other?

This question is slightly trickier, because the difference between the two angles isn’t so obvious. However, as evidenced by the image above, the blue angle could fit inside the yellow one with some leftover space. Therefore, the blue angle is smaller than the yellow angle.
Knife/sharp objects method

This technique is best suited for acute angle questions, although it can be helpful in certain right or obtuse angle questions. You must imagine that the angles are knife blades or other sharp, pointy objects. Then, try to determine which knife is the sharpest or pointiest. The sharper the “knife,” the smaller the angle; the less sharp (more broad) the “knife,” the larger the angle. As with the other methods, when you use the knife method, you’ll be visualizing the angles as real-life objects, which can help bring you closer to the correct answer.
Hill method

The hill method will require you to mentally orient the angles being compared in the same way. Remember that in the angle ranking section, the angles can be oriented any which way, so being able to mentally re-orient them might take some practice at first. Then, imagine that the angles are hills, and you are standing with your bike at the top. If you rode your bike down both hills, which would be the safer, less steep hill, and which would be more dangerous? Looking at the image above, Hill 1 is noticeably less steep than Hill 2, so you would be safer riding your bike down Hill 1. This means that the interior angle on the left is larger than the one on the right.
The hill method requires you to actually visualize yourself going down the “hill” formed by each angle, which can be useful if you’re feeling stuck.
- Compare to 90- and 180-degree angles.

For (almost) right angles
Imagine that you need to discern which blue angle is larger. Because both angles are relatively close to being right (90-degree) angles, you can compare both to perfect 90-degree right angles. Mentally draw in the dashed line shown, then see which is closer to being a perfect right angle. In the image above, the blue angle on the right is closer. Therefore, it must have a larger interior angle measurement than the blue angle on the left.
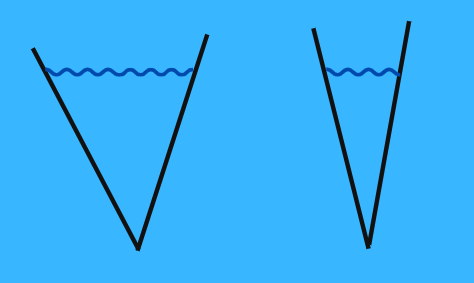
For very obtuse angles
In a similar way, you can compare obtuse angles to 180-degree straight lines. Take the example below:

Both of the blue angles above are very large, obtuse angles. But which is larger? By comparing to a straight line (180 degrees), and mentally drawing in or imagining the dashed line shown, you can see that the angle on the right is larger. It is closer to being a straight line than the angle on the left, so it must be the larger of the two angles.
- Use the answer choices to your benefit. Remember , the angle ranking questions, like all questions on the DAT, are multiple choice. Use this to your benefit! Some people are able to rank all four angles just by looking at them and then compare to the answer choices, but you often don’t need to be able to rank all the angles to find the correct answer. Looking at your answer choices first can actually be helpful. Imagine your answer choices are:
A. 1–2–3–4
B. 1–3–2–4
C. 3–1–2–4
D. 3–4–2–1
First, just figure out which angle is the smallest. Based on the answer choices, you’ll only need to compare Angles 1 and 3. Say you deem Angle 3 the smallest angle. Thus, eliminate A and B. Now, all you have to do to choose between answer choices C and D is determine which angle is the largest — Angle 4 or Angle 1. If you can figure that out, you’re done!
Practice using the answer choices and process of elimination to your benefit. In this example, by using the answer choices, you saved yourself the hassle of comparing all the angles, especially the tricky middle-ranking angles. All you had to do was figure out which angle was the largest and which was the smallest.
Here’s another example. Imagine these are your answer choices:
A. 1–4–2–3
B. 4–1–2–3
C. 1–2–3–4
D. 3–1–2–4
Imagine that, looking at the angles, you’re having a difficult time determining the ranking. However, you’re certain of one thing: Angle 2 is smaller than Angle 4. That means the correct answer choice MUST rank Angle 2 before Angle 4. Looking at the above answer choices, answers A and B can thus be eliminated, as both rank Angle 4 before Angle 2. By using your answer choices, you narrowed down the options by 50%. Now, even if you have to take your best guess, you have a 50% chance of choosing the correct answer!
- Manage your time. Aim to spend no more than 20–30 seconds on each angle ranking question. Don’t dwell on a question if you’re stumped — just mark it, take your best guess, and move on! And remember that speed comes with practice, so don’t be discouraged if you need much more time per question at the beginning of your preparation.
Angle ranking is all about practicing and developing the methods that work best for you. Try out the techniques above and see which ones feel the most natural to you, as these are the techniques that will help you do your best on test day. Wishing you the best of luck in your PAT preparation!
—
Join the Crack the DAT community, connect with other pre-dental students, and ask questions! Join the Facebook group here.
Crack your Dental Admission Test! Visit our website at CrackDAT.com.
